Programming with Python

Analyzing Data from Multiple Files

We now have almost everything we need to process all our data files. The only thing that's missing is a library with a rather unpleasant name:

import glob

The glob library contains a single function, also called glob, that finds files whose names match a pattern. We provide those patterns as strings: the character * matches zero or more characters, while ? matches any one character. We can use this to get the names of all the IPython Notebooks we have created so far:

print glob.glob('*.ipynb')

['01-numpy.ipynb', '02-func.ipynb', '03-loop.ipynb', '04-cond.ipynb', '05-defensive.ipynb', '06-cmdline.ipynb', 'spatial-intro.ipynb']

or to get the names of all our CSV data files:

print glob.glob('*.csv')

['inflammation-01.csv', 'inflammation-02.csv', 'inflammation-03.csv', 'inflammation-04.csv', 'inflammation-05.csv', 'inflammation-06.csv', 'inflammation-07.csv', 'inflammation-08.csv', 'inflammation-09.csv', 'inflammation-10.csv', 'inflammation-11.csv', 'inflammation-12.csv', 'small-01.csv', 'small-02.csv', 'small-03.csv']

As these examples show, glob.glob's result is a list of strings, which means we can loop over it to do something with each filename in turn. In our case, the "something" we want is the code that generates those plots of our inflammation data. Let's test it by analyzing the first three files in the list:

filenames = glob.glob('*.csv')
filenames = filenames[0:3]
for f in filenames:
    print f

    data = np.loadtxt(fname=f, delimiter=',')

    fig = plt.figure(figsize=(10.0, 3.0))

    axes1 = fig.add_subplot(1, 3, 1)
    axes2 = fig.add_subplot(1, 3, 2)
    axes3 = fig.add_subplot(1, 3, 3)

    axes1.set_ylabel('average')
    axes1.plot(data.mean(axis=0))

    axes2.set_ylabel('max')
    axes2.plot(data.max(axis=0))

    axes3.set_ylabel('min')
    axes3.plot(data.min(axis=0))

    fig.tight_layout()
    plt.show(fig)

inflammation-01.csv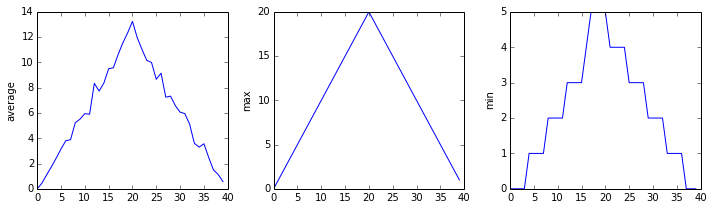

inflammation-02.csv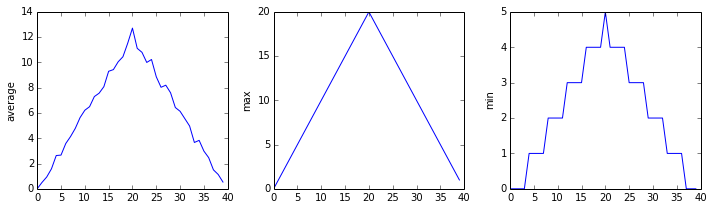

inflammation-03.csv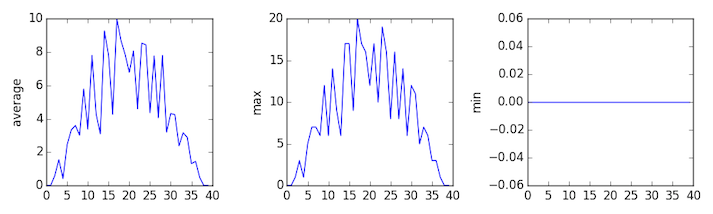

Sure enough, the maxima of the first two data sets show exactly the same ramp as the first, and their minima show the same staircase structure; a different situation has been revealed in the third dataset, where the maxima are a bit less regular, but the minima are consistently zero.